Science team at Berkeley Lab-based DOE science center unravels the mystery of a multiplier mechanism in an organic crystal
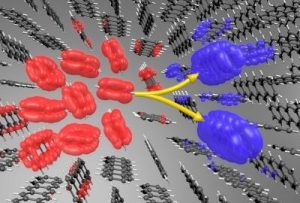
In this image, an optically excited spin-singlet state (red), which features electron-hole pairs, splits into a pair of spin-triplet states (blue). The individual triplets have equal and opposite center-of-mass momenta — they behave like waves moving in opposite directions along a crystal. The gray and white spheres represent carbon and hydrogen atoms, respectively.
While there is a growing market for organic solar cells ¬¬- they contain materials that are cheaper, more abundant, and more environmentally friendly than those used in typical solar panels – they also tend to be less efficient in converting sunlight to electricity than conventional solar cells.
Now, scientists who are members of the Center for Computational Study of Excited-State Phenomena in Energy Materials (C2SEPEM) a new energy materials-related science center based at the Department of Energy’s Lawrence Berkeley National Laboratory (Berkeley Lab), have solved a mystery that could lead to gains in efficiency.
They pinpointed the source of an ultrafast and efficient process that spawns several carriers of electrical charge from a single particle of light in organic crystals that are integral to this increasingly popular form of solar cells.
This process – called “singlet fission” because it is akin to the splitting of atomic nuclei in nuclear fission to create two lighter atoms from a heavier one – holds promise for dramatically boosting the efficiency of organic solar cells by rapidly converting more of sunlight’s energy to electrical charges instead of losing it to heat.
The research team found a new mechanism explaining how this reaction can occur in just tens of femtoseconds (quadrillionths of a second), before other competing effects can steal away their energy. Their study was published on Dec. 29 in the journal Physical Review Letters.
“We actually discovered a new mechanism that allows us to try to design better materials,” said Steven G. Louie, director of C2SEPEM, a DOE-supported center that includes researchers from Berkeley Lab; the University of California, Los Angeles; the University of Texas at Austin; and the Georgia Institute of Technology.
Louie, a co-leader of the study, is also a senior faculty scientist in Berkeley Lab’s Materials Sciences Division and a professor of physics at UC Berkeley. C2SEPEM focuses on developing theories, methods, and software to help explain complex processes in energy-related materials.
In the splitting process, a composite particle composed of an electron, which has a negative charge, and its partner hole – a vacant electron position in a material’s atomic structure that behaves like a particle in carrying a positive charge – rapidly converts into two electron-hole pairs. This doubles the charge-carrying potential in the material while avoiding the loss of energy as heat.
“There’s a lot we still don’t understand about the fundamental physics of this process in crystalline materials that we are hoping to shed more light on,” said Jeffrey B. Neaton, associate director of C2SEPEM, who co-led the study with Louie.
Neaton is also the Associate Laboratory Director for Energy Sciences at Berkeley Lab, the director of Berkeley Lab’s Molecular Foundry, and a physics professor at UC Berkeley. “The computational method that we developed is very predictive, and we used it to understand singlet fission in a new way that may allow us to design materials even more efficient at harvesting light, for example.”
Louie noted that many past efforts had focused on just a few molecules within the material – in this case, the crystallized form of pentacene, which is composed of hydrogen and carbon – to learn about these exotic effects. But such approaches may have oversimplified the effects driving singlet fission.
“There have been many theoretical efforts to try to understand what’s going on,” he said.
In this latest study, the research team began with a large-scale view of the overall structure of the crystallized pentacene, and particularly its symmetry – the repeating patterns in its atomic framework.
“It’s like trying to explain the ocean by either looking at it molecule by molecule, or looking at a whole wave,” said Felipe H. da Jornada, a co-lead author of the study with Sivan Refaely-Abramson. Both are postdoctoral researchers at Berkeley Lab and UC Berkeley and are also affiliated with C2SEPEM.
“Our approach directly captures the whole crystal,” no matter the size, he noted.
The team used calculations performed in part at Berkeley Lab’s Molecular Foundry, and supercomputing resources at the Lab’s National Energy Research Scientific Computing Center to develop, model, and test their new theories of the fission process.
“We believe these theories can also be applied to very different materials,” said Refaely-Abramson, “and in this sense, theory is very important.” Prior experiments had missed some of the important clues about the crystal structure’s role in the singlet fission mechanism.
The study concludes that in order to efficiently double these electron-hole pairs, the sampled material should display a specific kind of symmetry, or repeated combinations of molecules, within its crystal structure – just as a room’s floor can display a multitude of simple, repeating patterns using the same tiles.
The efficiency of the singlet fission process appears to rely heavily on the number of molecules packed within each repeating pattern or “motif” in the crystal, and on a particular type of symmetry that in which there is a 180-degree rotation and mirroring of these motifs. This relationship between symmetry and efficiency, the researchers found, allows them to make powerful predictions on the efficiency of the overall fission.
Those predictions can only be possible, though, if the electron-hole pairs in the sample behave as wavelike objects moving throughout the whole crystal like waves in an ocean. This approach also gave them new insight about the splitting process, and how the newly created pairs must behave like waves propagating in opposite directions.
There are still several steps that must be worked out to make these findings more relevant to real-world applications, the researchers noted. In solar cells, for example, electrons must be efficiently liberated from their pairing with holes to harvest their energy and improve solar panel performance.
Understanding the doubling of charge carriers in a material may help researchers to better explain and engineer reverse processes, too – such as the technology used in some mobile phone displays that reduces the number of charge carriers (a process known as triplet fusion), said Neaton.
Louie noted that the multidisciplinary team that was assembled for the study, a key aspect of the C2SEPEM center, was integral in introducing new thinking to address a decades-old problem.
“This is one of the first important topics that we could address, and now it’s come to fruition,” he said.
Story Source:
Materials provided by EurekAlert!.

